Theory

Model Reduction

The reduction method used for Attune is the modal method. In this method, the mode shapes of the nominal structure are used to reduce the structure. The resulting mass and stiffness are:

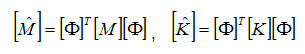
The reduced mass matrix is a diagonal matrix of modal masses. The reduced stiffness matrix is a diagonal matrix of modal stiffnesses. The reduced matrix sensitivities are calculated as follows:

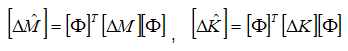
In general, none of the modal sensitivity matrices are diagonal.

When mass is allowed to vary, it is possible for the overall mass properties of the model to change. Attune tracks those properties. If M_r is the rigid body mass matrix and the sensitivity of the rigid body mass properties is given by deltaM_r, the updated mass properties are approximately given by M_r_new = M_r + sum(deltaM_r*deltaalpha). The mass properties are derived from M_r according to the following:

mass = trace(M_r(1:3,1:3))/3

Xcg = M_r(2,6)/mass

Ycg = M_r(3,4)/mass

Zcg = M_r(1,5)/mass

I = M_r(4:6,4:6)

Modal Calculations

For the modally reduced matrices, modal frequencies and shapes are calculated as follows:

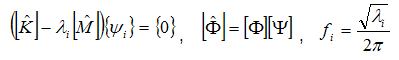
where 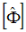are the eigenvectors of the reduced model in physical coordinates and 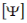are the eigenvectors of the reduced model in modal coordinates. All modes of the reduced model need to be calculated, even if only a subset are used as targets. For the nominal design case, the modal mass and stiffness matrices are diagonal and the eigenvalues are simply the ratio of modal stiffness to modal mass. To predict the fidelity of the model once the design has changed, however, the eigenvalue problem must be solved.

Cross-Orthogonality

The cross-orthogonality between a set of test mode shapes 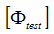and a set of analysis shapes 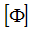is given as follows:

The orthogonality, therefore, requires a reduced-mass matrix whose DOF correspond to the physically measured DOF. In the case of modal reduction, that matrix is not available. Therefore, a Guyan-reduced-mass matrix is used instead, where the mass matrix is statically reduced to the measured DOF. The analysis shapes must likewise be reduced to the measured degrees of freedom. The analysis shapes are reduced using a Boolean matrix. The cross-orthogonality is a mass-weighted measure of the linear dependence of the test mode shapes on the analysis mode shapes.

Cross-MAC

The cross-MAC between a set of test mode shapes 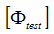and a set of analysis shapes 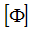is given as follows:

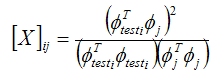
The MAC, therefore, requires mode shapes whose degrees of freedom correspond to the physically measured degrees of freedom (unless the test mode shapes are expanded). The analysis shapes are reduced using a Boolean matrix. The cross-MAC is a measure of the linear dependence of the test mode shapes on the analysis mode shapes. In Attune, to be more compatible with cross-orthogonality, the objective function uses the square root of the cross-MAC to define the error.

Sensitivity Calculations

All the model-update calculations in Attune are based on the sensitivity of some system parameter (e.g., stiffness, frequency, cross-orthogonality, cross-MAC) with respect to design variables. The modal matrix sensitivities are computed in Nastran using a finite difference approach. In a finite difference method, the design sensitivity is calculated by making a small (~1%) variation in each design variable and recalculating the required system parameter. The sensitivities of the modal parameters could also be computed analytically, as discussed in references 1, 2, and 3. These methods are usually more numerically efficient than the finite difference approach but may be less stable in the presence of closely spaced modes. To ensure robustness, Attune uses finite difference to compute sensitivities of modal parameters.

Optimization

The purpose of Attune is to find a set of design variable values which provides the highest correlation to the test with the smallest change in design variable values. Mathematically, the optimization problem can be expressed in the following quadratic form:

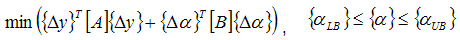
where 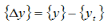is the difference between the current values of the state variables and the target values of the state variables, and 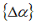is the change in design variables for the current iteration.

The state variables may be frequencies, cross-orthogonalities, modal assurance criteria, or frequency-response functions, but in all casesm the state variables can be expressed in terms of the nominal values, the design sensitivities, and the design variables as follows:

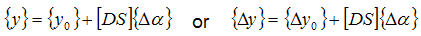
where 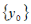are the values of the state variables immediately before the current iteration and 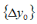is the error associated with 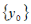. The objective function can then be written solely in terms of 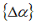as

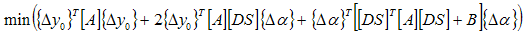
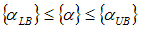
Note that mass property state variables are not normalized as are other variable types. It is therefore important to set weights for mass state variables to make sure they are appropriately scaled compared to other state variables.

RSS Option for Optimization

A common problem in mode shape optimization occurs when the model has repeated roots or very closely spaced modes [7]. This often occurs when the model has one or more axes of symmetry. In that case, the model can have multiple mode shapes at the same (or nearly the same) frequency representing motion that is symmetric about an axis. More generally, this problem can occur when models have repeated roots from any source: symmetry, multiple identical components, or high modal density. The eigensolution for a problem with repeated roots is not unique. This means that, for the set of repeated roots, the eigensolver can return any set of vectors which spans the space of those roots. Any linear combination of those vectors is also a solution. This causes a problem because the solution provided by the analytical model may not agree with the modes derived from the test even if the analytical model is exact. Since it is only necessary to obtain a model whose mode shapes span the test shapes, we need a metric that measures how well a set of analysis modes space spans the test shapes for repeated roots.

This is what is done with the RSS option. However, a straightforward RSS cannot be used as a metric for orthogonality here. If we assume that v is a vector containing the part of the cross-orthogonality matrix corresponding to a particular test mode and the set of repeated roots from the analysis model that are meant to span that mode, the RSS would be given as:

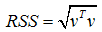
Because the analysis modes are not exactly orthogonal to the reduced-mass matrix used to compute the cross-orthogonality, this formula for RSS could result in values greater than 1.0. To compensate for the lack of orthogonality with respect to the reduced-mass matrix, we have introduced an extra term to the RSS:

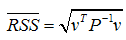
where P is a partition of the self-orthogonality matrix corresponding to the repeated roots. If necessary, a Moore-Penrose pseudoinverse is used for robustness. This metric varies between 0.0 and 1.0, with a value of 1.0 indicating that the test mode can be expressed as a linear combination of the repeated roots of the analytical model.

An example of this phenomenon can be seen in primary bending modes of a cylinder. Since the cylinder is axially symmetric, there are two primary bending modes whose motions are in orthogonal directions, but which can combine to represent a primary bending mode in any lateral direction. The orientation of such modes observed in a test may not correspond to the orientation obtained from analysis. In fact, a model with a pair of symmetric modes could exactly match the test data and have a cross-orthogonality as low as 70%. Without any method for addressing repeated roots, an optimization algorithm would try to change the model to improve the cross-orthogonality even though there was effectively no error. In Attune, with the RSS option enabled, errors due to different orientations are ignored.

Gradient-based Optimization

Gradient-based optimization seeks to solve the minimization problem posed in the previous section by computing the gradient of the objective function. Because the equation includes sensitivities of the state variables with respect to the design variables, the derivatives of the modal parameters discussed in previous sections must be approximated based on the modal matrix sensitivities.

The gradient-based optimization must solve the following equation:

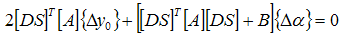
subject to the constraints

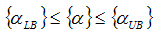
One method for solving the constrained optimization problem is the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method. This method, while originally suited for large-scale, unconstrained nonlinear optimization problems, can be altered for constrained problems. The method is a quasi-Newton method similar to a steepest descent method. Instead of relying on only the first derivative, the use of a Hessian updating method to scale the steepest descent direction can help eliminate the possibility of stagnation. Specifically, the steps are as follows:

1. Estimate initial design and Hessian matrix.

2. Compute search direction and step size.

3. Update design and update Hessian approximation.

4. Repeat steps two and three until convergence.

The strength of this method is the use of second-order derivatives. While a pure Newton method would be impractical because of the large number of calculations required to compute the exact Hessian at each iteration, the BFGS method uses an approximation that greatly reduces the number of calculations required without significantly sacrificing accuracy.

Genetic Algorithm Optimization

The GA seeks to minimize the same objective function as in the gradient optimization. However, the approximate sensitivities of the modal parameters are not necessary. The GA evaluates a set of randomly chosen designs against the objective function and then tries to systematically improve the designs through iteration.

The first step in a GA is to discretize the design space. For this optimization scheme, the design variables must be bounded. Each design variable is allowed to take on a discrete number of values within the specified range. The designs are encoded as binary numbers. The number of discrete values that a design variable can take on is determined by the number of bits, N, used for that variable (2N values). For example, a design variable discretized using 4 bits can take on 16 values. The resolution, the distance between discrete points, is given by

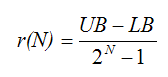
where UB is the upper bound and LB is the lower bound.

The next step in the GA is to create an initial population and evaluate the population against the objective function. In general, the computational cost and quality of the result both increase as a function of the population size. An empirical study showed that a population size of 4L would be effective where L is the total number of bits used to discretize the design [4].

Once the population has been evaluated, the designs are made to compete against one another in a two-round tournament (tournament selection). In each round, two designs are chosen at random and their objective function values compared. The design with the lower objective function value is added to the winner population. This type of selection process has two certain outcomes: the design with the minimum overall objective function value will always be chosen, and the design with the maximum overall objective function value will never be chosen.

After selection, the GA performs crossover. There are several forms of crossover; two popular forms are referred to as uniform crossover and single-point crossover. For uniform crossover, two designs are chosen at random from the winner population. From these two designs, two “children” designs will be generated. For each bit of the design, it is randomly determined which child will receive the bit from which parent. For example, there is a 50% chance that parent 1’s first bit will go to child 1. If it does, child 2 gets its first bit from parent 2. If it does not, child 1 gets its first bit from parent 2 and child 2 gets its first bit from parent 1. This is repeated for all bits.

The process for single-point crossover is similar except that the designs of the children are not randomly chosen bit by bit. Instead, a single random number determines the point at which crossover occurs. In other words, if the design is made up of 10 bits and the crossover point is 4, child 1 would be a copy of parent 1 for bits 1–4 and a copy of parent 2 for bits 5-10. Similarly, child 2 would be a copy of parent 2 for bits 1-4 and a copy of parent 1 for bits 5-10. Because single-point crossover is more likely to leave large portions of the design intact, it is considered a more aggressive method, whereas uniform crossover is considered more exploratory.

There is one further step before the next generation is complete: mutation. Mutation is the process by which new genetic material is added to the population. This is useful in case the initial population did not contain the part of the design space which included the global minimum. For uniform mutation, there is a specified probability that any bit in the design population could flip. The default mutation probability is 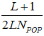, where L is the total number of bits used in the design and NPOP is the size of the population. A higher mutation rate would be more exploratory, and a lower rate would be more aggressive.

An often-used option with GA is called elitism. This option allows the best design(s) to propagate forward to the next generation without crossover or mutation. This guarantees that the GA will have monotonic convergence; however, it also effectively diminishes the population size by the number of elite members.

Composite Sensitivity

The composite sensitivity is a metric for determining the relative sensitivity of the active state variables to the design variables. The metric is based on the objective function for optimization. For a single design variable, the composite sensitivity is given by

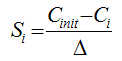
where C_init is the value of the objective function for the current design with the overall design weight set to 0.0, and Ci is the value of the objective function with the ith design variable changed by ∆.